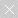“不要把鸡蛋放在同一个篮子里”,这是关于资产配置最耳熟能详的一句话,但资配远没有这么简单。
今天,新方程资配投资经理,就从经典的资配模型,带你走进资产配置的历史变迁,分享如何才能让你的资产配置“活”起来。
资产配置是投资绕不开的一个课题,有效的资产配置方案能够有效改善投资组合的风险收益特征。
如何做好资产配置?
这一问题持续伴随着投资持续专业化的发展路径,不同的时期,有不同的解决方案。虽然这些方案有着不同的着眼点,底层逻辑也有较大的区别,但是这些都反映着专业投资者的一个共同的信念:
只有通过资产配置,才能助财富穿越亦明亦暗的历史长河。
纵观资产配置理念和方法论的进化史,同所有理论一样,资产配置也经历了从稍显简陋,到日臻完善的发展路径。
总结下来,主要有三方面的变化:
1、从聚焦Beta到兼顾Alpha;
2、从经验主义勾勒风险到科学系统地降低波动;
3、从关注单一资产风险到同时注重降风险下的收益获取。
本文笔者也主要从这三个方面,依次分析几种历史上比较重要的资产配置方案。
均值方差模型
最早的时候,资产配置理念并未跟数学走得很近,人们的对于资产配置的思想也比较朴素,就是"不把鸡蛋放在同一个篮子里",哪个篮子放多少也只是根据以往的经验和波动来主观确定。
例如我们熟知的二八组合,投资者会将20%的资金配权益,80%的资金配债券,相对静态、机械地平衡单一资产的波动。然而这就有几个比较明显的问题:为什么是二八比例,底层数理逻辑是什么?加入其他类资产会如何变化?如何动态去调整来应对尾部风险?等等。
为了解决以上问题,也为了更科学地理解探究资产配置的有效性,业界持续从数理、历史分析的角度研究有效的资产配置方案,直到上世纪六十年代,哈利马科维茨提出来现代投资组合理论,资产配置才真正有理论可依,马科维茨也被称为现代投资组合之父。
马科维茨的理论并不深奥,但很优雅,用数学模型来表达的就是均值方差模型,数学表达式如下:
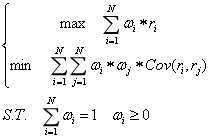
其中wi中为第i个资产的权重,Cov(ri, rj)为第i个资产和第j个资产收益率的协方差。
原始均值方差模型为最大化组合收益,同时最小化组合风险。因此,原始均值方差模型为两目标优化问题,优化的结果是一条曲线,即Pareto有效前沿。投资者可根据自己的风险承受能力,确定对应风险下的最大化收益及配置方案。
所有理论和思想都是持续完善的,原始均值方差模型也有弊端。
从数学表达上我们也可以看出来,仅仅依靠各资产的历史相关性和历史收益率就能有效确定未来有效的组合配置?那当未来宏观环境变化造成资产定价逻辑的阶段性变化后,历史还能不能指引未来?答案大概率是否定的,至少是不完美的。多数时间,我们很难完全相信历史,对于某类资产或者多类资产,我们也会有自己的观点,诸如,资产A我认为接下来大概率有10%的涨幅,或是资产A较资产B大概率会表现更优等等。那,如何将这些观点,融入传统的优化问题中?
这的确是一个比较有吸引力的事情,这也是BL模型出现的初衷。
BL 模型
BL 模型是马尔科维茨均值方差模型的一种进化模型,其核心理念为将主观观点与市场均衡收益相结合:通过输入使用者的相对或绝对观点,以及观点对应的置信度,用贝叶斯压缩的方式改变资产的历史分布,然后再进行优化求解。得出既满足资产的历史表现,又迎合我们投资观点的组合配置方案。
从上述讲解上也可以发现,BL模型的数理逻辑链条要复杂得多,涉及到很多参数和中间环节运算,本文暂且不表。
风险平价模型&最大分散化模型
均值-方差模型和BL模型考虑的是风险和收益的折中的理念(即给定风险,最大化收益,或给定收益最小化风险),除此以外,也有更侧重于关注风险的资产配置模型,例如风险平价、最大分散化等模型。
相较于传统的Markowitz均值-方差模型,风险平价模型只关注风险。同时由于均值-方差模型只考虑组合整体的风险,从而经常出现风险被某一资产完全控制的现象(与投资分散化理论相悖),风险平价模型可以有效解决该问题。风险平价模型的宗旨是使得所有资产对投资组合的风险贡献相等,数学表达如下:
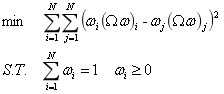
其中,资产权重为w,投资组合收益率协方差矩阵为?。上述可以理解成确定一组资产权重,使得各资产对组合的风险贡献相等。然而确定权重的过程需要依赖函数寻优来进行,对每个资产的风险贡献两两求差值,再将平方值进行加总即可得到优化函数。理想情况下,该优化函数最优解一定是各资产风险贡献相等时取最小值,并且为0,这同风险平价原理一致。
除了风险平价,关注风险分散的模型还有最大分散化模型,其数学表达为:
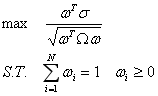
最大分散化模型的目的是极大化投资组合的分散程度,该模型的核心思想是:如果投资组合中各资产完全相关(各资产的相关系数=1),则组合的风险最大;而当各资产的相关性越来越弱,则组合的风险也会越来越小。最大分散化模型的目标就是极大化这种相对分散的效果,即最大化加权平均波动率与整体投资组合波动率之间的“距离”,来创建最分散的组合。
其他模型
除了以上讲的多种资配模型,还有从他们的思想基础上,衍生出的一些比较经典的模型:
例如分层风险平价模型,在风险平价模型的基础上对各资产进行聚类,然后再通过聚类结果进行风险权重分配;
再比如风险预算模型,人为先预估各资产在组合中的风险贡献比例,然后再通过历史相关性进行寻优逼近,生成投资组合。
以上多数配置模型仅依赖历史相关性、波动性、收益等量化信息,部分会加入一些主观观点,但多也只是基于波动和收益的,其它维度的有效信息并未考虑。但资产价格的影响因素是多维度的,例如宏观状态、行业基本面信息、市场情绪等。
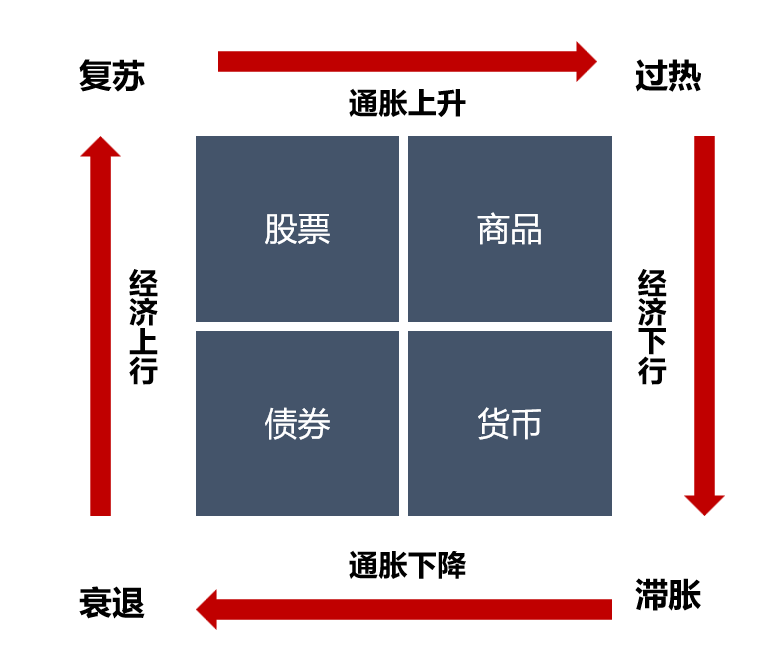
所以除了上述的一些偏定量、偏Beta的模型,还有部分偏主观、偏轮动的模型。比如我们前期分析过的美林时钟,通过历史归纳和逻辑分析,得出不同宏观状态下的有效资产,然后进行资产配置,也是一种比较经典的资产配置思路。其它如普林格六周期模型、货币-信用周期模型,也是一些比较经典的偏主观的资产配置模型。
让资配保持生机
但如何在琳琅满目的资产配置方案中,选择符合投资者资产管理目标的资配方案是比较困难的。
因为不管是传统的均值方差模型,还是后来的风险平价模型,亦或是新兴的加入宏观因子从因子层面上考量资产配置的新兴方案,都不具有普适性。其资配结果既依赖于资配方案本身的数学原理,又依赖于底层标的特性、市场的轮转以及宏观经济的变化。
一个成功的资产配置方案的,仅有资产配置模型是不够的,更需要我们在传统的资配理念之上,加入对底层具体标的的认知,以及对投资组合的动态维护。
而这,需要我们提升自己对资产的认知,在传统的资配模型的思想上再进行一次方法论“封装”,才能使旧的资配思想保持生机。
风险提示:
投资有风险。基金的过往业绩并不预示其未来表现。基金管理人管理的其他基金的业绩并不构成基金业绩表现的保证。相关数据仅供参考,不构成投资建议。投资人请详阅基金合同等法律文件,了解产品风险收益特征,根据自身资产状况、风险承受能力审慎决策,独立承担投资风险。
重要提醒:
本文版权为新方程所有,未经许可任何机构和个人不得以任何形式转载和发表。